圖片來源：BakaArts for Quanta Magazine

數學家的夢之國

在一個(ge) 名為(wei) Zulip的線上論壇上，一群誌同道合的數學家幾乎每天都會(hui) 聚在一起創造他們(men) 所堅信的“未來”。他們(men) 都是Lean這個(ge) 軟件程序的狂熱信徒。原則上來說，Lean是一個(ge) “證明助手”，能幫助數學家完成證明過程。但是在Lean能獨當一麵之前，數學家們(men) 得親(qin) 自將數學輸入到程序中，將積累了數千年的數學星空体育官网入口网站翻譯成Lean能理解的語言形式。

“顯然，當你將某個(ge) 事物數字化後，你就可以通過新方式利用它了，”倫(lun) 敦帝國理工學院的Kevin Buzzard說道，“（所以）我們(men) 要對數學進行數字化，讓它變得更好。”

一直以來這都是數學家們(men) 的夢想。他們(men) 預期的好處既包括用計算機給學生作業(ye) 打分、給期刊審稿、替代人力完成一項證明中冗長重複的細節等等這樣平凡的任務，也包括利用人工智能來發現新數學領域、為(wei) 舊問題找新解這樣宏偉(wei) 的目標。

但是首先，在Zulip上集結的數學家們(men) 必須給Lean提供相當於(yu) 一個(ge) 圖書(shu) 館級別的大學數學星空体育官网入口网站，可他們(men) 現在隻完成了一半。Lean短期內(nei) 還不能解決(jue) 開放性問題，但從(cong) 事該項目的人幾乎可以肯定，在幾年內(nei) ，這個(ge) 程序將至少能理解大三期末考試題的數學問題了。

漫長的訓練之路

為(wei) 了訓練Lean，他們(men) 把整個(ge) 夏天都貢獻了出去：一群經驗豐(feng) 富的Lean用戶開設了一個(ge) 名為(wei) “好奇數學家的Lean”線上研討會(hui) 。在第一部分，澳大利亞(ya) 悉尼大學的Scott Morrison展示了如何在程序中完成一個(ge) 證明過程。

他首先用Lean能理解的語言輸入他想證明的定理。比如說，“素數無限定理”。現在有多種方法可以證明這個(ge) 定理，但Morrison希望對公元前300年歐幾裏得發現的第一種證明方法進行微調。這種方法通過將已知的全部素數相乘後再加一形成新的素數對定理進行了證明。Morrison的選擇反映出使用Lean的基本要求：用戶不得不獨立想出自己的辦法。

在輸入題目、選擇完解題策略之後，Morrison花費了幾分鍾的時間展示證明的結構：他定義(yi) 了一係列相對容易證明的中間步驟。雖然Lean無法找到一個(ge) 證明的總體(ti) 策略時，它常常能幫助執行小而具體(ti) 的步驟。在將證明過程分割成可管理的子任務的過程中，Morrison有點像一個(ge) 廚子，指揮著一線廚師切洋蔥、然後慢燉出一道美食。Morrison指出，“到了這個(ge) 節骨眼上，你就可以期待Lean接管大局成為(wei) ‘掌廚’，開始提供真正的幫助。”

Lean通過使用稱為(wei) “策略”的自動化流程來執行這些中間任務。而這些“策略”可以被當作用於(yu) 執行特定工作的短算法。

證明過程中，Morrison通過運行“數據庫搜索（library search）”的策略算法搜索庫中的數學結果並反饋一些數學定理填補到具體(ti) 的證明過程中。一種名為(wei) “linarith”的策略算法可以接收關(guan) 於(yu) 兩(liang) 個(ge) 實數的不等式並確認有關(guan) 第三個(ge) 數的新不等式的正確性。例如：如果a等於(yu) 2，而b大於(yu) a，那麽(me) 3a+4b大於(yu) 12。其他策略算法可將基本代數規則如結合率等進行應用。

Morrison總共用了20分鍾來完成歐幾裏德的證明。他自己在一些地方添加了細節，而另一些地方則是策略算法幫他完成的。Lean對每一步都進行了檢查來確保他的工作與(yu) 程序潛在的邏輯規則一致。

“這如同一款數獨App。如果你的某一步是無效的，那它就會(hui) 出問題，”Buzzard評論道。最終，Lean證明Morrison的證明過程有效。

不過歐幾裏德的證明過程已經存在了兩(liang) 千多年。而數學家們(men) 目前關(guan) 心的問題太複雜以至於(yu) Lean還不能理解問題，更別說為(wei) 它們(men) 的解答過程提供支持了。

“很可能還得過10多年它才成為(wei) 一個(ge) 研究工具，”Lean用戶，美國福特漢姆大學的Heather Macbeth認為(wei) 。

因此，Lean還需學習(xi) 更多數學。這看似是個(ge) 簡單的任務——隻需將數學課本翻譯成Lean可以理解的形式就行了。但不幸的是，很多數學星空体育官网入口网站並不存在於(yu) 教科書(shu) 中，所以這項工作並不簡單。

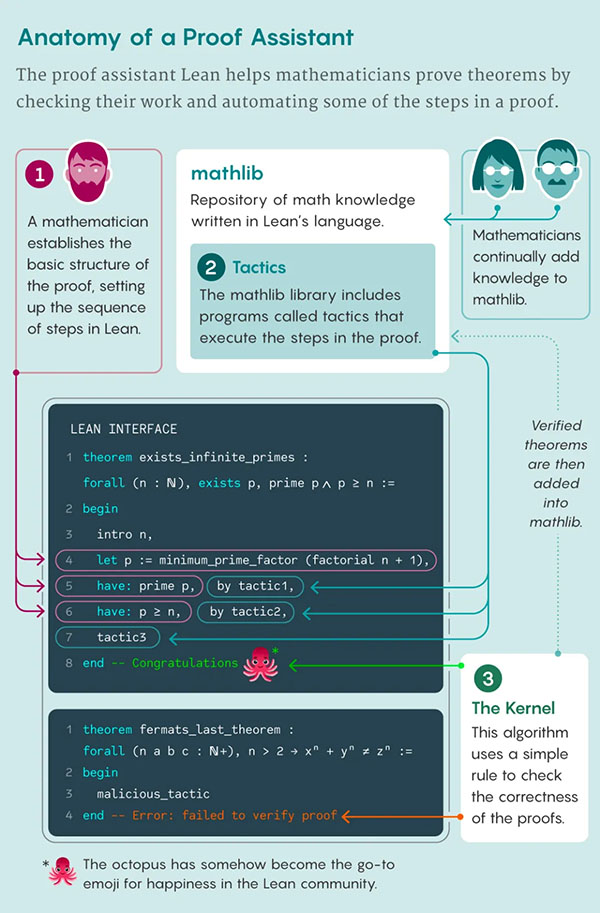
圖解證明助手。 （圖片來源：Samuel Velasco/Quanta Magazine）

散落的星空体育官网入口网站

事實上，高中和大學數學、甚至很多研究生學到的數學隻是微不足道的一小部分。數學的絕大部分內(nei) 容還不夠係統化。

大量重要的數學星空体育官网入口网站從(cong) 未被詳細完整地記錄下來，它們(men) 隻存在於(yu) 少數人的頭腦裏，幾乎是民間傳(chuan) 說一樣的存在。

還有一些領域，雖然基本材料記錄完備，但內(nei) 容過於(yu) 龐大複雜，人們(men) 無法檢查它們(men) 的正確性。然而，數學家們(men) 卻對此信心十足。

“我們(men) 相信作者的聲譽。我們(men) 知道他是個(ge) 認真的天才，那麽(me) 他的證明或理論一定是正確的，”巴黎-薩克雷大學的Patrick Massot說。這也是為(wei) 什麽(me) “證明助手”（計算機輔助證明）如此誘人的一個(ge) 原因。將數學翻譯成一種計算機能理解的語言鞭策著數學家們(men) 對星空体育官网入口网站進行最終分類和精確定義(yi) 。

法國國家研究院的Assia Mahboubi意識到了這個(ge) 數字化數據庫的潛能，“我覺得很有趣。從(cong) 理論上講，一個(ge) 人可以通過純粹的邏輯語言，捕獲全部數學文獻，並在計算機中存儲(chu) 一個(ge) 能夠用程序檢索和查證的數學語料庫。”

前車之鑒

其實，Lean並不是第一個(ge) 有這種潛能的程序。世界上第一個(ge) 計算機輔助證明程序是上個(ge) 世紀六十年代發行的Automath。而1989年發行的Coq則是目前使用最廣泛的“證明助手”程序。

直到2013年，微軟研究員Leonardo de Moura才創造了Lean。他本希望該程序可以成為(wei) 檢查軟件代碼準確性的工具，而非用於(yu) 數學。但檢查軟件的準確性與(yu) 數學證明所用的思路十分類似。

因此，數學家們(men) 很快被這個(ge) 新程序所吸引。他們(men) 在數學領域上提出的擴展問題耗費了de Moura大量時間。據Morrison描述，忍無可忍的de Moura對數學家們(men) 說，“你們(men) 這群家夥(huo) 為(wei) 什麽(me) 不創建一個(ge) 單獨的數據存儲(chu) 庫？”

於(yu) 是，數學家們(men) 在2017年創建了名為(wei) mathlib的數據庫並開始迫切地向其中填補世界上的數學星空体育官网入口网站，努力將它打造成21世紀的亞(ya) 曆山大圖書(shu) 館（曾擁有西方世界最豐(feng) 富的古籍收藏）。他們(men) 創建並上傳(chuan) 了許多數字化的數學星空体育官网入口网站片段，逐漸構造出一個(ge) 供Lean參考的目錄。新構建的mathlib得以讓數學家們(men) 從(cong) Coq等舊係統的局限性中吸取教訓並學會(hui) 留意對材料的組織方式。

最大的數學圖書(shu) 館

Mathlib的首頁可以顯示項目進展的實時數據，還記錄著已被數字化的數學星空体育官网入口网站總量。10月初時，Mathlib已經包含18,416條定義(yi) 和38,315個(ge) 定理。

利用Lean，數學家們(men) 可以將這些原料混合在一起創造新的數學星空体育官网入口网站。不過現在，mathlib還隻是個(ge) 有限的“原料儲(chu) 存室”。它幾乎不包含高等數學多個(ge) 領域常用的複雜分析和微分方程的內(nei) 容，甚至無法陳述出任何一個(ge) 美國克雷數學研究所（CMI）提出的千禧年大獎難題。

但是它在慢慢填補著星空体育官网入口网站空白。在Zulip上，數學家們(men) 不停地標示出需要創建的定義(yi) ，並且自願編寫(xie) 它們(men) 並及時為(wei) 彼此的工作提供反饋意見。

“任何一個(ge) 數學研究者在mathlib上都能發現幾十個(ge) 需要補充的定義(yi) 或定理，”Macbeth說，“所以你決(jue) 定填補這些漏洞。這能帶來即時滿足感。別人看到後會(hui) 在 24 小時內(nei) 評論。”

今年夏天的研討會(hui) 上，法國裏昂高等師範學院的Sophie Morel發現很多補充內(nei) 容都是一小部分。作為(wei) 練習(xi) ，會(hui) 議組織者給參與(yu) 者提供了一些相對簡單的數學陳述讓他們(men) 使用用Lean證明。在思考其中一個(ge) 問題是，Morel 意識到她的證明需要用到一個(ge) mathlib沒有收錄的引理（為(wei) 了取得某個(ge) 更好的結論而作為(wei) 步驟被證明的命題）。於(yu) 是，她就自己給這個(ge) 引理寫(xie) 了三行代碼。

當然，也有一些重量級的貢獻。去年，Gou?zel在為(wei) mathlib研究幾何學和拓撲學中有重要作用的“光滑流形”的定義(yi) 。

他認為(wei) ，雖然基礎定義(yi) 隻有一個(ge) ，但對於(yu) 更複雜的對象，可能有10到20種不同的方式使其形式化。為(wei) 了在特殊性和普遍性中間找到平衡，他最後寫(xie) 出了1,600行代碼。

給收錄對象在普遍性水平上找到合適的定義(yi) ，無疑是構造mathlib的數學家們(men) 的主要工作。他們(men) 希望現在的研究對將來都有用。

通往真正的數學研究之路

圖片來源：Pixabay

為(wei) 了證明Lean能夠處理數學家們(men) 真正關(guan) 心的問題，德國弗賴堡大學的Buzzard，Massot，和Johan Commelin在去年開始了一項宏偉(wei) 的概念證明項目。目標是給21世紀數學界最偉(wei) 大的發明——完備空間（perfectoid space）做一個(ge) 數字化定義(yi) 。

他們(men) 將三千多個(ge) 其他數學對象的定義(yi) 與(yu) 它們(men) 之間存在的三千多個(ge) 聯係相結合。這些定義(yi) 涉及多個(ge) 數學領域，從(cong) 代數到拓撲再到幾何。它們(men) 被逐步整合成一個(ge) 單一對象的定義(yi) ，這個(ge) 過程生動地展現出數學是如何隨時間變得越來越複雜的，也表明了正確奠定mathlib的基礎有多麽(me) 重要。

最終，他們(men) 成功進行了概念證明，定義(yi) 了完備空間。不過，要確切表達完備空間中出現的數學問題，Lean還有很多星空体育官网入口网站需要學習(xi) 。

雖然Lean成為(wei) 真正的數學研究工具還需漫長的時間，但這並不意味著這個(ge) 程序是個(ge) 不可實現的概念。數學家們(men) 正努力在數學數字化的路上鋪設第一條鐵軌，雖然他們(men) 可能沒有機會(hui) 親(qin) 自搭乘最終跑起來的那班列車。

作者：Kevin Hartnett

翻譯：王千玥

審校：魏瀟

引進來源：Quanta Magazine

引進鏈接：https://www.quantamagazine.org/building-the-mathematical-library-of-the-future-20201001/