會員登錄
我們(men) 一般都是1年會(hui) 過1次生日，比如你的生日是8月21日，每年都會(hui) 有一個(ge) 8月21日，這就代表了你每年都會(hui) 過1次生日。
可是，你應該聽過閏年這回事吧。如果你聽過的話，那麽(me) 你應該也知道，會(hui) 有這樣一種“倒黴”的人，他出生在2月29日，這個(ge) 日期每4年才會(hui) 出現1次。所以嚴(yan) 格地說，他每4年才會(hui) 過1次生日。
因為(wei) 每4年會(hui) 有1個(ge) 閏年，閏年就是說這1年裏麵一共有366天，比平時多1天。多的這1天就被加在了2月份，於(yu) 是就有了這個(ge) 2月29日。
可是為(wei) 什麽(me) 會(hui) 有閏年呢？如果每年都是365天不是更方便嗎？如果那樣的話，也就不會(hui) 有這種倒黴的人，每4年才能過1次生日。
要回答這個(ge) 問題，我們(men) 需要先搞明白到底什麽(me) 是1年，什麽(me) 是1天。我們(men) 平時認為(wei) 的，1年就是春夏秋冬的1次交替，1天就是日升日落的1次循環。這都是正確的，不過卻並不準確。更準確的說法是地球繞著太陽1圈的時間是1年，地球自轉1圈的時間是1天。
我們(men) 都知道，地球在自己旋轉的同時也會(hui) 繞著太陽公轉。那麽(me) 是不是說，平時地球繞太陽1圈正好地球自己旋轉365圈，而每隔四年，地球公轉的時間就會(hui) 變長，變成了366天呢?
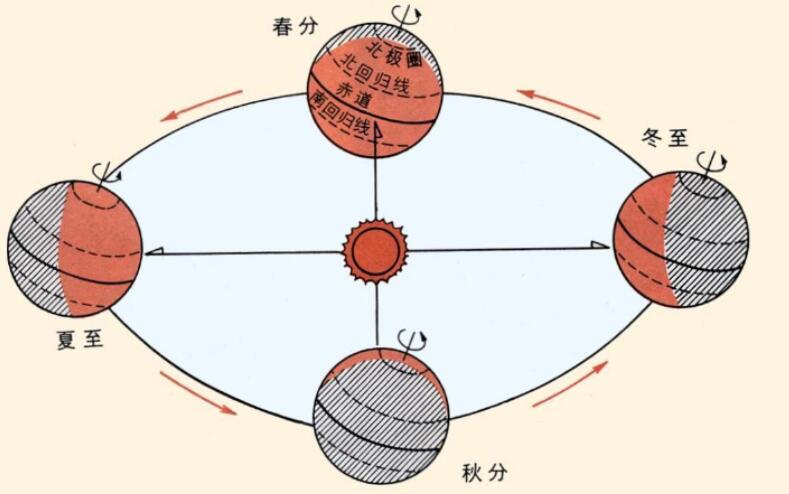
這樣的想法很有道理，但是並不是實際情況。地球公轉所用的時間是不會(hui) 發生改變的，不論是4年還是100年，它都是公轉1圈要花365天5小時48分鍾46秒。而平時日曆上記錄的1年肯定都是整數的天數，所以我們(men) 就規定1年有365天的時間。這樣的規定，一開始是沒有問題的，因為(wei) 對於(yu) 1年來說，相差個(ge) 幾小時根本不算什麽(me) 。可是隨著時間地推移，每年就會(hui) 少將近6個(ge) 小時的時間，4年下來就會(hui) 少了差不多1天了，100年後會(hui) 少差不多一個(ge) 月，如果時間再長一些，可能每年的12月份就變成了放暑假的時間了。
所以，為(wei) 了彌補每年會(hui) 少差不多6個(ge) 小時這個(ge) 問題，就又繼續規定，平時1年是365天，但是每隔4年會(hui) 增加1天，把積累起來的少記錄的1天時間給補上，於(yu) 是就是366天了。
可是這就完了嗎？並沒有。如果1年的時間是365天6小時整，那麽(me) 這樣的軌道是沒有問題的。但是，實際情況卻不是這樣，這就導致了按照新的規定，每4年所以記錄的時間又會(hui) 增加那麽(me) 一點點。這樣的誤差如果長年累月累計起來，最後也會(hui) 出現問題。於(yu) 是隻能繼續增加規定，平時1年是365天，每隔4年會(hui) 增加1天，但是每100年又會(hui) 少記錄1天的時間。
當然即使這樣軌道，問題仍然沒有最終解決(jue) ，還是會(hui) 有誤差。於(yu) 是可以繼續規定：前麵的規定繼續保留，然後每400年再繼續增加1天。其實，如果認真起來的話，這個(ge) 規定是可以無限下去的。不過，我們(men) 並不需要規定那麽(me) 多，現在這樣的規定上千年才會(hui) 出現一天的誤差，完全可以滿足我們(men) 日常的需要，所以也就不再繼續規定下去了。
歡迎掃碼關(guan) 注深i科普！
我們(men) 將定期推出
公益、免費、優(you) 惠的科普活動和科普好物！
深圳市龍華區玉翠社區高坳新村小廣場
- 參加最新科普活動
- 認識科普小朋友
- 成為科學小記者
