版權歸原作者所有，如有侵權，請聯係我們(men)

中國古代數學源遠流長，成書(shu) 於(yu) 漢代的《九章算術》曆來被稱作“算經之首”，是其中最重要的一部數學著作。

正如已故中國科學院院士、著名數學家吳文俊先生（1919-2017）所言：“《九章算術》及其劉徽注，對數學發展在曆史上的崇高地位，足可與(yu) 古希臘歐幾裏得《幾何原本》東(dong) 西輝映，各具特色。”

那麽(me) ，《九章算術》究竟有哪些數學成就，又為(wei) 何在數學史上有如此高的地位，今天一起來看看。

算籌與(yu) 準十進製位值製記數法

數字的表達是人類理解世界的重要方式。成書(shu) 於(yu) 漢代的《九章算術》總結了先秦以來的數學成就，其記載的最重要一項數學成就是算籌的準十進製位值製記數法。

所謂十進製（decimal system），就是從(cong) 1 開始記數，到 10 就換一個(ge) 記數方式；所謂位值製（place-value system），就是同樣一個(ge) 數字放在不同位置，就具有不同的數量含義(yi) 。古埃及數學采用的是十進製記數法，但並非位值製（實是壘數製）；古巴比倫(lun) 數學采用的位值製記數法，但其使用的是 60 進製。現代同行的印度-阿拉伯數字是十進製位置值，而從(cong) 文獻的記載來看，晚於(yu) 中國算籌記數。因此，新加坡學者藍麗(li) 蓉（Lam Lay Yong）甚至提出印度-阿拉伯數字乃起源於(yu) 中國算籌的說法。2016 年，中國科學院自然科學史研究所編《中國古代重要科技發明與(yu) 創造》明確將這一成就列入其中。

算籌在中國行用長達約 2000 年，是在 16 世紀被算盤取代前中國人長久以來使用的數學工具，也是日本、朝鮮、越南、琉球等漢字文化圈國家長久使用的數學工具。其材質一般用竹（也偶有象牙、骨、鉛、銀），漢代約長 12 厘米。近代以來多有算籌出土，1983 年 11 月在陝西省旬陽地區漢墓出土了 28 根象牙算籌。日本也藏有算籌。在古語中“筭”與(yu) “算”不同。前者的意思是擺弄竹子，即算籌；後者是裝算籌的器物，引申為(wei) 計算。因此在古書(shu) 中普遍寫(xie) 作“筭術”（即運用算籌的算法），例如《九章筭術》。

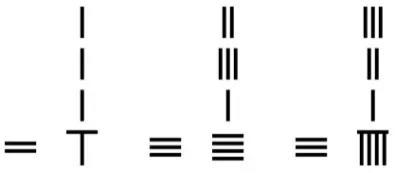
算籌記數分為(wei) 縱橫兩(liang) 式，其個(ge) 、百、萬(wan) 等位上用縱式，其十、千、百萬(wan) 等位上用橫式。如 12345，就擺放成

由於(yu) 其十位上的 1 和個(ge) 位上的 1 擺放不同，故筆者稱之為(wei) “準位值製”。這恰恰體(ti) 現了算籌記數的特點和優(you) 勢，由於(yu) 遇 0 是作空位處理，故這一縱橫不同可以最大限度凸顯空位，如：

表示 203

而不可能是 23（）。《九章算術》卷八方程涉及到正負術，以算籌的顏色和擺放亦可區分正負。

以算法為(wei) 中心

《九章算術》中的術

《九章算術》分成九卷，包含 246 個(ge) 數學問題。一直以來，學界有一種誤解認為(wei) 該書(shu) 是一本應用問題集。其實，246 個(ge) 問題對應的算法（即術）僅(jin) 有約 100 個(ge) ，經常出現多個(ge) 問題對應一個(ge) 算法的情況。因此，數學史家郭書(shu) 春指出該書(shu) 是采取“術文統率例題”的形式。

又有一種誤解認為(wei) ，該書(shu) 是一本算法操作手冊(ce) ，運籌者無須理解其中的數學原理。對此，數學史家李繼閔指出算法實施的過程中蘊含著算理（即“寓理於(yu) 算”），故不懂數學原理實際無法計算。

吳文俊先生高屋建瓴地指出中國古代的算法具有構造性和機械化的特點。所謂構造性，與(yu) 現代存在性數學相對應，指其算法往往給出求解路徑，而機械化則就其籌算過程而言。法國學者林力娜（Karine Chemla）通過大量細致地文獻分析，指出該書(shu) 及其劉徽注的數學問題、圖和棊等幾何工具以及算籌的實施，實際都是展現算法的工具，從(cong) 而有力地證明了以《九章算術》為(wei) 代表的中國古代數學是以算法為(wei) 中心的數學。

從(cong) 世界數學史的角度看，除了古希臘數學以外的其他數學文明都具有算法傾(qing) 向，丹麥數學史家休儒（Jens Høyrup）則進一步認為(wei) 中國數學是所有文明中最重視算法的。學界以往多認為(wei) 《九章算術》具有實用性和社會(hui) 性的特點，其實這一特點其他數學文明也均具備，唯有對算法的高度重視是中國古代數學獨特的，就此而言《九章算術》可視作一本理論數學著作。

《九章算術》卷一方田給出了籌算分數的計算法則和各種田麵積的計算公式，其中有圓麵積公式“半周乘半徑得積步”（即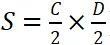），這一公式巧妙地回避了圓周率，故是完全準確的。

卷二粟米給出了各種穀物的換算，其中提出“今有術”，即已知三個(ge) 數求成比率的第四個(ge) 數，這一算法在西方被稱作“三率法”。

卷三衰分是講各種物品的比例分配問題。

卷四少廣涉及到對土地的丈量和劃分，其中給出了用算籌開平方和開立方算法，這一方法在宋代發展成普遍地求任意一元高次方程數值解的算法，與(yu) 現代數學中的牛頓法類似。

卷五商功是工程問題，涉及各種幾何體(ti) 的體(ti) 積計算問題，其中提出三種基本幾何體(ti) （即立方、塹堵和陽馬）以作為(wei) 求解任意幾何體(ti) 體(ti) 積的基礎。所謂立方，就是正立方體(ti) ；所謂塹堵，就是底麵為(wei) 等邊直角三角形的三棱錐，兩(liang) 塹堵合成一立方；所謂陽馬，就是底麵為(wei) 正方形，一棱與(yu) 底垂直的四棱錐，三陽馬合成一立方。

卷六均輸是關(guan) 於(yu) 稅收的比例分配問題。

卷七盈不足是通過兩(liang) 次假設求解問題的算法，該算法在西方被稱作“雙假設法”。又由於(yu) 該法可以把任何問題都理解成線性問題，進而求出解答，故也稱為(wei) 萬(wan) 能算法。

卷八方程是求解多元一次線性方程組的完整算法，其中給出了涉及該問題時必須用到的正負術法則。例如第一問：

今有上禾三秉，中禾二秉，下禾一秉，實三十九鬥；上禾二秉，中禾三秉，下禾一秉，實三十四鬥；上禾一秉，中禾二秉，下禾三秉，實二十六鬥。問：上、中、下禾實一秉各幾何。荅曰：上禾一秉九鬥四分鬥之一，中禾一秉四鬥四分鬥之一，下禾一秉二鬥四分鬥之三。

按術列出如下方程，其求解過程類似亦類似現代的矩陣方程解法。清末現代數學傳(chuan) 入中國以後，李善蘭(lan) 借用古語“方程”翻譯 equation，實際是改變了方程的原意。

卷九勾股是講平麵圖形的麵積計算問題，其中給出了勾股定理及其各種變化形式。

給出算法正確性的論證

劉徽注《九章算術》

《九章算術》文本中隻給出算法，而沒有其正確性的證明，這一點在以往是被當作中國數學不如以《幾何原本》為(wei) 代表的古希臘數學的證據。現代數學史研究表明這一觀點是完全站不住腳的。

其一，除了古希臘數學以外的數學文明，往往都隻給出算法而沒有證明。故吳文俊先生認為(wei) 數學史是算法傾(qing) 向與(yu) 演繹傾(qing) 向兩(liang) 大主題此消彼長形成的。

其二，文本中有沒有證明實際是取決(jue) 於(yu) 文本的性質和所產(chan) 生的語境，換言之文本中沒有證明不代表數學實踐中也沒有證明。

其三，林力娜等學者認為(wei) 不應以古希臘的數學證明作為(wei) 證明的唯一形態，在其他文明中也有不同形態的證明。第二第三點恰巧從(cong) 劉徽注中可以獲得驗證。

魏景元四年（ 263 ），劉徽注解了《九章算術》，對大部分術文都給出其算法正確性的論證。尤其是，在卷一對圓麵積公式的證明、卷四對球體(ti) 積公式的注解、卷五對陽馬體(ti) 積的證明中用到極限逼近的推理方法，展現了極高的邏輯推理能力。在卷四求解球體(ti) 積公式的過程中，劉徽發明出牟合方蓋，但卻無法求出其體(ti) 積，故“以俟能言者”。這一問題最終被祖衝(chong) 之父子解決(jue) 。劉徽對幾何問題的證明需用到圖（平麵問題）和棊（立體(ti) 問題），其推理原理被吳文俊總結為(wei) “出入相補原理”。

《九章算術》的影響與(yu) 曆史地位

《九章算術》在唐宋均作為(wei) 國子監算學館的教科書(shu) 。劉徽之後，唐李淳風、北宋賈憲、劉益、蔣周、南宋秦九韶、楊輝、金李冶、元朱世傑等均沿著《九章算術》的路線發展中國古代數學，並使其在宋元時代達到一個(ge) 高峰。明清時期，中國數學發展的主流改變，但《九章算術》的整體(ti) 框架並未改變。日本數學則在中國宋元數學的基礎上發展出和算，在 19 世紀時可以處理麵積求和等微積分初等問題。

自李儼(yan) （1892-1963）、錢寶琮（1892-1974）先生開創中國數學史研究以來，《九章算術》及其後世的注解就作為(wei) 中國數學成就的標誌性著作，但他們(men) 主要關(guan) 注其中與(yu) 現代數學可以相通之處。其實，《九章算術》中那些獨特算法同樣是中國數學的偉(wei) 大成就。兩(liang) 者共同說明了中國數學曆史道路的獨特性和其曆史經驗的有效性。

吳文俊先生把中國古代數學的算法理解成計算機的軟件、把算籌、算盤等工具理解成計算機的硬件，從(cong) 而創造性地提出數學機械化的構想，這是中國古代數學“古為(wei) 今用”的典範案例。

策劃製作

本片為(wei) 科普中國·創作培育計劃扶持作品

出品丨中國科協科普部監製丨中國科學技術出版社有限公司、北京中科星河文化傳(chuan) 媒有限公司

作者丨朱一文 科學技術史博士，中山大學哲學係教授、博士生導師，邏輯與(yu) 認知研究所專(zhuan) 職研究員

策劃丨林林

責編丨林林 鍾豔平

審校丨徐來

歡迎掃碼關(guan) 注深i科普！

我們(men) 將定期推出

公益、免費、優(you) 惠的科普活動和科普好物！