我想你肯定好奇過，地圖上很少有形狀規則的國家，那麽(me) 這些國家的麵積是怎麽(me) 測量出來的呢？特別是在沒有計算機技術的年代？

今天就通過一個(ge) 勺子，來解答你的這個(ge) 疑問。

關(guan) 鍵概念

斧狀求積儀(yi)

材料和操作

一根木棍

2個(ge) 不同重量的鐵釘

或者一個(ge) 金屬湯勺

製作很簡單，隻要一根木棍，兩(liang) 端分別釘入2個(ge) 重量不同的鐵釘就可以了，其中一個(ge) 鐵釘要特別重一點，盡量讓棍子的重心靠近這個(ge) 釘子。

做成差不多這樣子——

這個(ge) 數學工具最有意思的地方在於(yu) 它的使用過程。

1 把輕的釘子放在圖形的邊緣上的一點B，重的釘子放在C點。

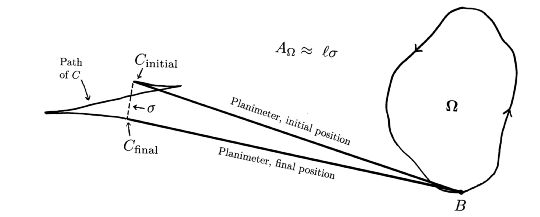
2 B沿著圖形移動，最後回到起始點。

3 量一下C的起始和最終位置間的距離 D。量一下棍子本身的長度 L。

圖形的麵積 ≈ L × D

如果你不想做一個(ge) 斧狀求積儀(yi) ，用一個(ge) 比較重的金屬勺子也可以代替。

看下麵這個(ge) 捷克的網友 Robert Mařík 用同樣的測量方法，計算四分之一個(ge) 圓的麵積。

按照他的測量，勺子求積儀(yi) 測得的麵積是0.75，和積分法算得的麵積（π/4）的誤差約為(wei) 5%。

你還可以利用各種材料製作斧狀求積儀(yi) ——

瑞士軍(jun) 刀也行——

原理

美索不達米亞(ya) 的粘土片和埃及的莎草紙證明，人類很早就開始處理麵積的問題。

美國第16次人口普查（1940 - 1941年）時，工作人員利用求積儀(yi) 計算麵積。

@The U.S. National Archives

大約在2百年前，人類發明出了能準確計算不規則圖形麵積的方法，它就是求積儀(yi) 。求積儀(yi) 是通過畫形狀邊界線的方式計算麵積的數學工具，主要分成兩(liang) 種。

第一種求積儀(yi) 再沿著邊界線滑動的過程中，通過積分來計算麵積。這類工具常常用來測量不規則的圖形，某個(ge) 城鎮的麵積，或者用來測量機器的效率。這類求積儀(yi) 的計算比較準確。

機械求積儀(yi)

@AMS

另一類求積儀(yi) 雖然也繞著形狀邊緣畫線，但是它對麵積僅(jin) 僅(jin) 進行了估算。我們(men) 製作的斧狀求積儀(yi) 就屬於(yu) 這類。

20世紀初製造的斧狀求積儀(yi)

@Bob Otnes

斧狀求積儀(yi) 是丹麥數學家，騎兵軍(jun) 官 Holger Prytz 在1875年發明的。1887年，丹麥哥本哈根的 Cornelius Knudsen 公司就開始製造斧狀求積儀(yi) 。

實際上早在1814年，就有人發明了求積儀(yi) ，後來瑞士數學家 Jakob Amsler-Laffon 在1854年發明的第一類求積儀(yi) 已經比較接近現代版本了。

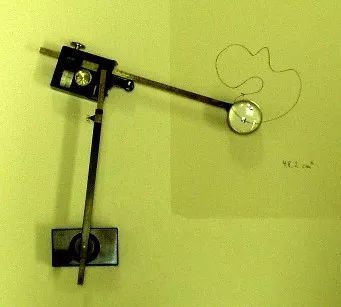
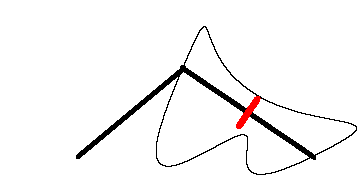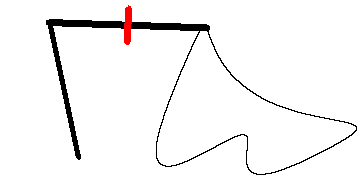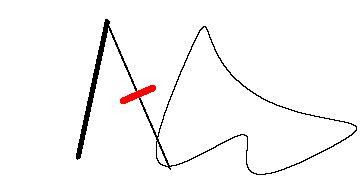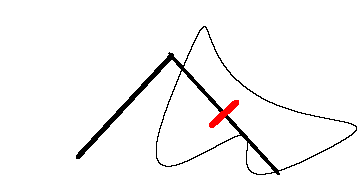
瑞士數學家 Jakob Amsler-Laffon 在1854年發明的求積儀(yi)

但是 Prytz 的版本更加經濟方便，雖然比 Amsler 的求積儀(yi) 要不準確一些。

那麽(me) ，斧狀求積儀(yi) 是怎麽(me) 算出圖形麵積的呢？

從(cong) 數學上來說，斧狀求積儀(yi) 首先利用曳物線（簡單來說，一個(ge) 物體(ti) 被另一個(ge) 物體(ti) 用棍子拖著走時，領先的那一端畫出的曲線）對導數進行了近似，並且利用格林公式（Green’s theorem）來求解麵積。

麵積 ≈ 重的那一頭的位移 × 斧狀求積儀(yi) 的長度。

不過，斧狀求積儀(yi) 是近似求解麵積，它存在誤差。誤差和斧狀求積儀(yi) 的長度，以及你畫圖時的方向（順時針還是逆時針）有關(guan) 。我們(men) 看這樣一個(ge) 例子。

@wabash.edu

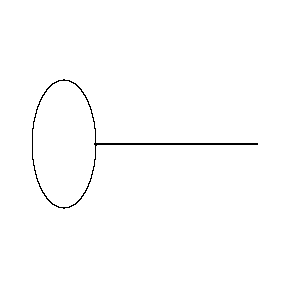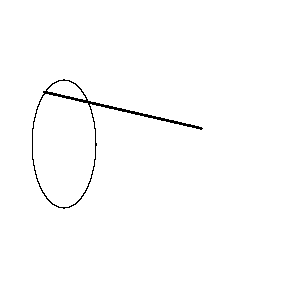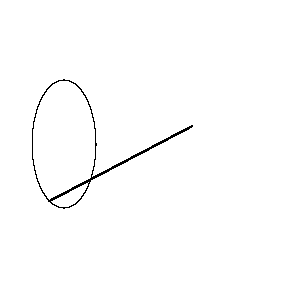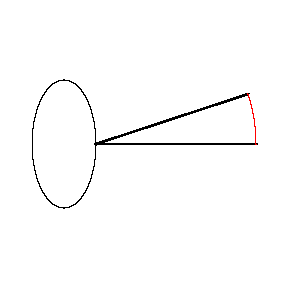
假設斧狀求積儀(yi) 繞著橢圓轉了一周。橢圓的長徑是4，短徑是2，斧狀求積儀(yi) 的長度是5，重的那點移動的距離是紅色的這一段圓弧。

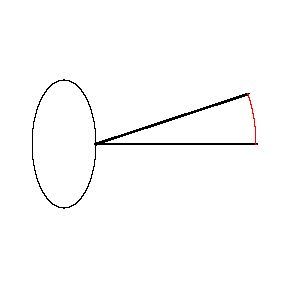
紅色圓弧的長度是1.59，因此用斧狀求積儀(yi) 計算得到的橢圓麵積是：

1.59 × 5 = 7.94。

直接用橢圓的長徑和短徑和算得的橢圓麵積是2π，也就是6.28。誤差達到了26%。

這是為(wei) 什麽(me) 呢？

這是因為(wei) 斧狀求積儀(yi) 相對於(yu) 要計算的麵積太短了。如果用長度為(wei) 10的斧狀求積儀(yi) 來測量，那麽(me) 得到的麵積是7，誤差縮小至11%；如果用長度為(wei) 20的斧狀求積儀(yi) 測量，那麽(me) 求得的麵積是6.62，誤差隻有5.3%。

實際上，誤差和斧狀求積儀(yi) 的長度約成反比，因此用較大的斧狀求積儀(yi) 測量比較小的麵積會(hui) 更準確。

另外，斧狀求積儀(yi) 旋轉的方向對測量結果也有影響。如果長度為(wei) 5的斧狀求積儀(yi) 從(cong) 同一個(ge) 起點，用順時針繞著同樣的橢圓旋轉，那麽(me) 測得的麵積是6.77，誤差是7.8%，比逆時針時要小。

再來看看斧狀求積儀(yi) 沿著其他規則形狀得到的軌跡——

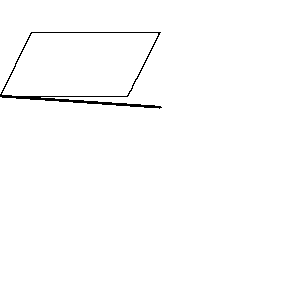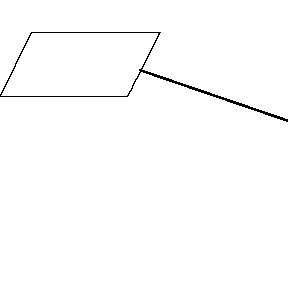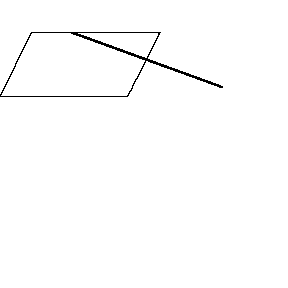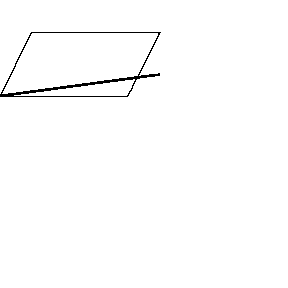
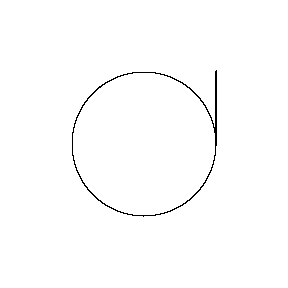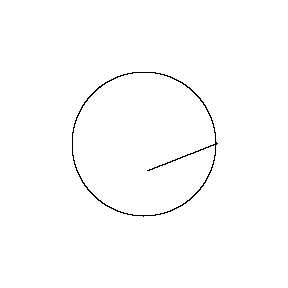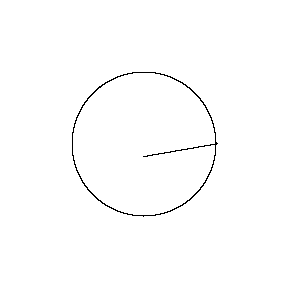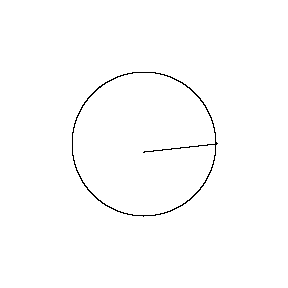
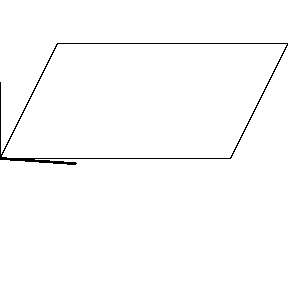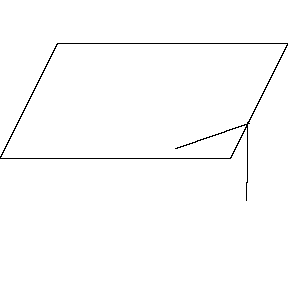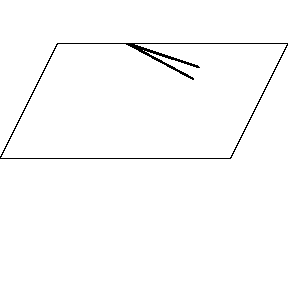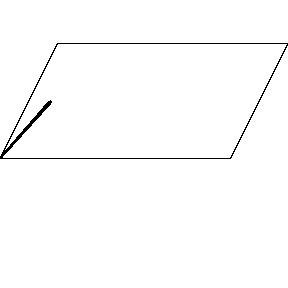
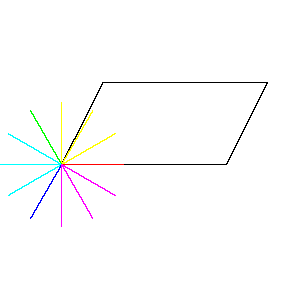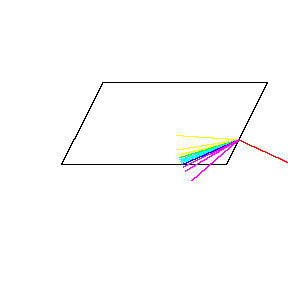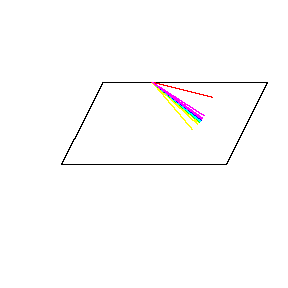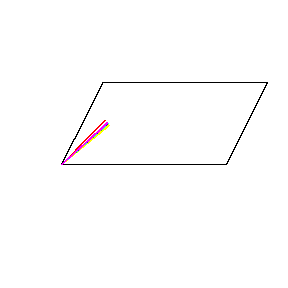
@wabash.edu

測量房間麵積的新技能get✔：沿著房間四角爬一圈。

然後用身高乘以 jio 的移動距離。

僅(jin) 適用於(yu) 姚明，否則誤差太大。

關(guan) 注【深圳科普】微信公眾(zhong) 號，在對話框：
回複【最新活動】，了解近期科普活動
回複【科普行】，了解最新深圳科普行活動
回複【研學營】，了解最新科普研學營
回複【科普課堂】，了解最新科普課堂
回複【團體(ti) 定製】，了解最新團體(ti) 定製活動
回複【科普基地】，了解深圳科普基地詳情
回複【科學防控】，學習(xi) 疫情相關(guan) 科普星空体育官网入口网站
回複【科普小達人】，報名參賽贏取萬(wan) 元大獎