圖1、圖2為(wei) 《勾股容圓》紀念封。（圖片由中國集郵有限公司提供）

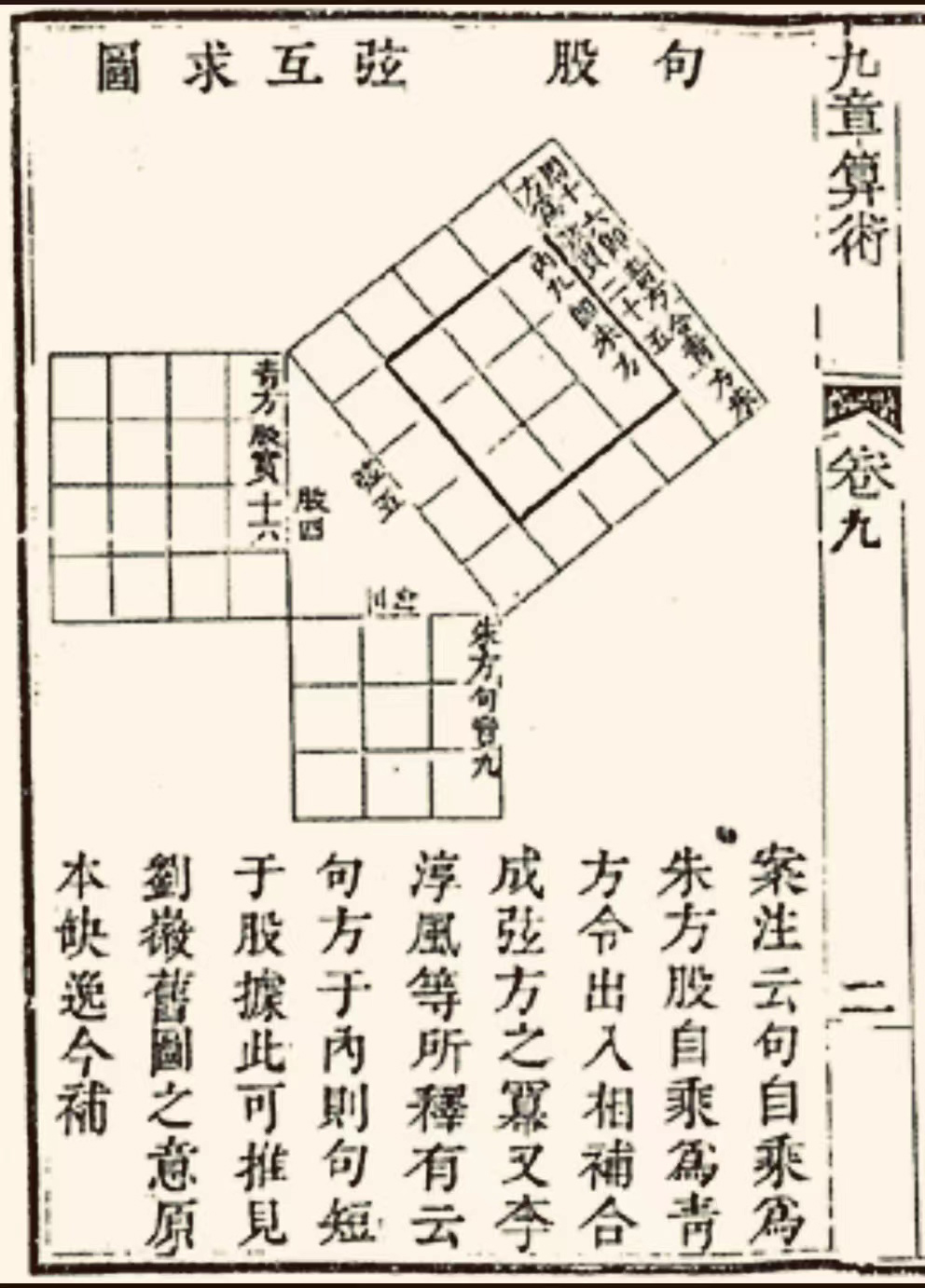
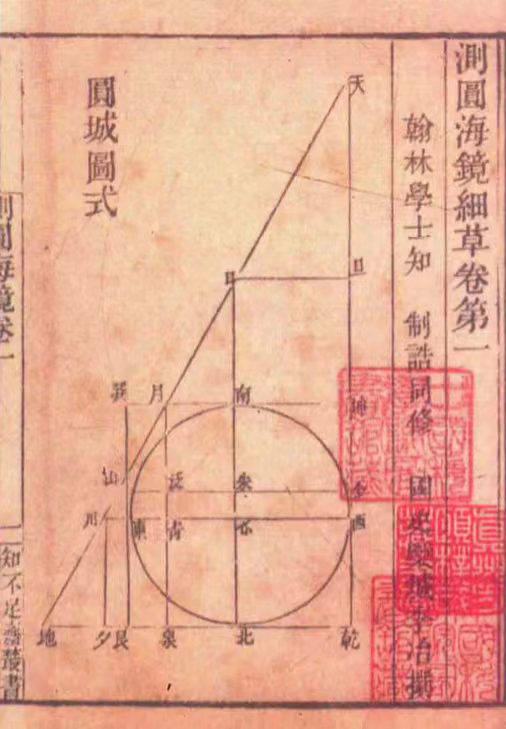
圖3、圖4、圖5、圖6分別為(wei) 《周髀算經》《九章算術》《測圓海鏡》《則古昔齋算學》的書(shu) 影。（圖片由作者提供）

據漢代《周髀算經》記載，昔者周公問算於(yu) 商高，商高對曰：“勾廣三，股修四，徑隅五。”周公讚曰：“大哉言數。”

古人以“勾三股四弦五”為(wei) 上聯，有對仗下聯“六詩七絕八古”者，也有巧對“碧草玉蘭(lan) 修竹”者，又何其美哉言數也！

漢代《九章算術》勾股章第16題“今有勾八步，股十五步。問勾中容圓，徑幾何？”

該題“術文”為(wei) “八步為(wei) 勾，十五步為(wei) 股，為(wei) 之求弦。三位並之為(wei) 法，以勾乘股，倍之為(wei) 實。實如法，得徑一步。”三位即勾、股、弦，若分別以a、b、c表示，則此圓徑d=2ab／a+b+c。

此開勾股容圓問題研究之先河。勾股容圓是通過勾股形（今稱直角三角形）和圓的各種相切關(guan) 係求圓直徑的問題，這是中國數學史上的一個(ge) 重要問題。

魏晉時期的劉徽用出入相補原理和率的理論（借助衰分術）兩(liang) 種方法證明了這個(ge) 公式。

宋金時期，洞淵在此基礎上研究了同一個(ge) 圓和各種勾股形的相切關(guan) 係，給出了由勾股形的三邊求圓徑的9個(ge) 公式，稱為(wei) “洞淵九容”。洞淵是道教的派別，通“九數”，活躍於(yu) 唐宋。

元代李冶由洞淵九容演繹成《測圓海鏡》，不僅(jin) 保留了洞淵九容公式，即9種求直角三角形內(nei) 切圓直徑的方法，而且給出一批新的求圓徑公式。

卷一“圓城圖式”：“假令有圓城一所，不知周徑。四麵開門，門外縱橫各有十字大道。其西北十字道頭，定為(wei) 乾地；其東(dong) 北十字道頭，定為(wei) 艮地；其東(dong) 南十字道頭，定巽地；其西南十字道頭，定為(wei) 坤地。所有測望雜法，一一設問如後。”此為(wei) 《測圓海鏡》170問的總題設：今正方形乾坤巽艮容一圓，圓與(yu) 15個(ge) 勾股形的各種關(guan) 係，由此展開。

這是全書(shu) 的總括圖解，由一個(ge) 直角三角形、它的內(nei) 切圓以及一些特定的點和直線組成。其中的頂點、圓心和交點都用某個(ge) 漢字來指代，相當於(yu) 西方用字母，有異曲同工之妙，是為(wei) 李冶的創造。

卷一“識別雜記”闡明了圓城圖式中各勾股形邊長之間的關(guan) 係以及它們(men) 與(yu) 圓徑的關(guan) 係，共600餘(yu) 條，每條可看作一個(ge) 定理（或公式），這部分內(nei) 容是對中國古代關(guan) 於(yu) 勾股容圓問題的總結。

後麵各卷的習(xi) 題，都可以在“識別雜記”的基礎上以天元術（解方程）為(wei) 工具推導出來。李冶總結出一套簡明實用的天元術程序，並給出化分式方程為(wei) 整式方程的方法。他發明了負號和一套先進的小數記法，采用了從(cong) 零到九的完整數碼。除零以外的數碼古已有之，是籌式的反映。但籌式中遇零空位，沒有符號“0”。從(cong) 現存古算書(shu) 來看，李冶的《測圓海鏡》和秦九韶《數書(shu) 九章》是較早使用0的兩(liang) 本書(shu) ，它們(men) 成書(shu) 的時間相差不過一年。《測圓海鏡》重在列方程，對方程的解法涉及不多。但書(shu) 中用天元術導出許多高次方程（最高為(wei) 6次），給出的根全部準確無誤，可見李冶是掌握高次方程數值解法的。

總之，李冶在勾股容圓術中有專(zhuan) 門的概念和公式，采用了演繹推理的方法，這在中國數學思想發展史中占有重要的地位。

中國宋元時期，研究測圓術的數學家不在少數。比如朱世傑的《四元玉鑒》中有“勾股測望”門，其中就有這方麵的題目。比如有一題是這樣的：“今有圓城，不知大小，各中開門。甲、乙俱從(cong) 城心而出，甲出南門一十五步而立；乙出東(dong) 門四十步見甲。問城周幾何？”

後世學者對《測圓海鏡》給予高度的評價(jia) 。清代阮元認為(wei) 《測圓海鏡》是“中土數學之寶書(shu) ”；《則古昔齋算學》的作者李善蘭(lan) 稱讚它是“中華算書(shu) 實無有勝於(yu) 此者”，又補充了3種容圓關(guan) 係：勾弦上容圓，股弦上容圓，弦外容圓。

（作者係國家教育谘詢委員會(hui) 委員，中國科技館原館長、研究員）

歡迎掃碼關(guan) 注深i科普！

我們(men) 將定期推出

公益、免費、優(you) 惠的科普活動和科普好物！